

by Ping · Updated December 16, 2023

On my first day as a math teacher, I was worried chaos would reign supreme. My nerves were shot and the students were chatty. How is there any chance that class would go right?
But I had a secret weapon: lesson planning.
With any new situation in life, I try to go in over-prepared. And preparing my lessons in advance gave me the confidence I needed to teach effectively. With all my materials in order, I was able to track progress and get feedback to improve my teaching methods.
This article covers the essential elements of a math lesson plan and gives you tips to engage and educate your students.
Get my free resource library with digital & print activities—plus tips over email.
Lesson planning is crucial to align classes with the curriculum and standardized assessments, reduce classroom chaos, and improve teaching methods through reflecting and adapting to students' needs.
Here’s a few ways that lesson planning can make your class better:
This is why lesson planning is useful for teachers of all skill levels — and absolutely mission critical for first-year first teachers.
A high-quality math lesson plan leverages clear objectives, up-to-date content, real-world examples, and a variety of pathways to understanding.
First and foremost, a high-quality lesson plan starts with solid content.
Clear objectives ensure that your content aligns with your curriculum and supports student needs. Use current examples and avoid outdated materials to keep students focused.
Don’t forget to anticipate student questions and address them upfront to reduce confusion and increase engagement.
Next, high-quality lesson plans move beyond the word problems, and engage students by providing real-world examples and applications.
For example, a lesson plan might word problems based on their students’ favorite sports teams or players, or explore the geometry involved in designing clothing for students interested in fashion.
This way, students see the practical applications of the material and stay engaged in learning.
Lastly, high-quality lesson plans aim to engage all students, including those who aren't confident in math, with various ways to understand the material.
For example, they might integrate art and music or explore math problems without numbers to provide more approachable ways to connect with material.
Additionally, they create ways to differentiate within class, using self-checking activities and checks for understanding to identify opportunities to reteach for students that need extra support.
A math lesson plan includes lesson objectives, time planning, and procedures. It will leverage assessments to track progress and enable differentiation.
Objectives give students and teachers a clear understanding of what they need to accomplish. They should be specific and measurable, and align with state standards and curriculum goals.
For example, a clear objective for a lesson on fractions could be "Students will be able to add and subtract fractions with unlike denominators using the least common multiple." This would align with the Common Core State Standards for Mathematics 5.NF.A.1 and 5.NF.A.2.
Pacing is crucial to staying on track each lesson as well as covering your curriculum pacing for the year.
As you plan your lesson, make sure to have more than enough content to keep fast finishers engaged, and have an idea of what parts to cut if you're running over.
If you're just starting out, it's also worth time planning using bottom-up estimation, where you break down your lesson plan’s procedures section into small chunks and add time estimates to each. This makes it easy to reflect on where your estimates could be improved.
The procedures section of a plan outlines the play-by-play of your lesson. A few common components that I use in my lesson plans include hooks, guided notes, checks for understanding, practice, real-life applications, and reflections.

Hooks capture students' attention, introduce the topic, and create a sense of relevance.
A hook can take many forms, such as a story, a video, or a real-world example. For instance, a teacher might introduce a lesson on ratios and proportions by showing a video about how to use ratios to scale recipes.
Whatever the hook, it should be engaging and create a connection between the students and the material.
Looking for ideas on writing hooks? Check out my post, 7 Engaging Hooks for Your Math Lesson Plans.
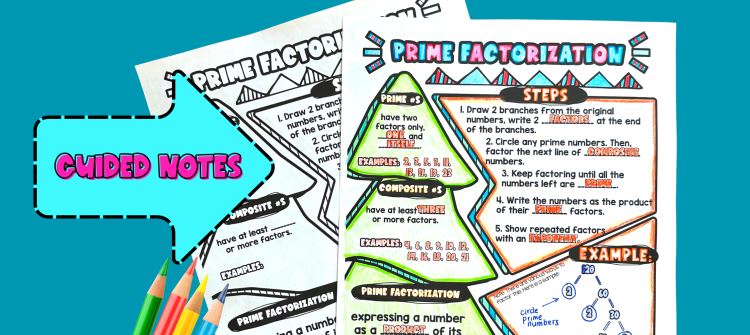
Guided notes are a powerful tool for direct instruction in middle school math.
They provide structure and help students take organized notes that are easy to follow during class and review later at home. High-quality guided notes are visually engaging and illustrate the concepts being taught.
For example, if teaching a lesson on graphing linear equations, a good guided notes template might include pre-drawn coordinate planes with labeled axis and sample equations that students can graph using the template.
By providing a clear framework for note-taking, guided notes help students better understand and retain the material being taught.

A check for understanding is a type of informal assessment used to verify student progress in a lesson.
For example, a teacher may ask students to explain how to solve a particular problem or work through a problem on the board. Real-world examples can be used to make these assessments more engaging and relatable for students, such as using a recipe to teach ratios or a sports scenario to teach probability.
These informal assessments help spot areas to reteach the whole class or a subset of students that are struggling.

Practice in class doesn’t just help with understanding, but is also a great moment for differentiation.
This can take many forms, from traditional worksheets to more creative approaches like art projects or digital activities.
For example, if teaching a lesson on algebra, students might use technology to complete digital pixel art in Google Sheets. By providing a variety of pathways to understanding, teachers can ensure that all students are engaged and motivated to learn.
Additionally, practice time is a great moment to pull students out for reteaching while fast finishers move onto more difficult activities.

Real-life applications connect math to the real world and make math meaningful for students.
For example, a lesson on fractions could include baking a cake to illustrate the concept of dividing ingredients, while a lesson on geometry could involve designing a garden to teach students about angles and shapes.
By providing real-world examples, students are more likely to stay engaged and see the practical applications of the material they are learning.

Student reflections provide valuable feedback to adjust future lessons.
For example, a math teacher might have students rate their understanding of the day's concept on a scale of 1-3 at the end of class or ask students to write down one thing they learned and one thing they still have questions about.
By collecting this data, teachers can adjust their lessons based on student needs and ensure that all students are able to keep up with the pace of the lesson.
It’s important to incorporate and plan for assessments continuously you’re writing your lesson plan.
There's two types of assessments to consider: formative and summative. You’ll want incorporate formative assessments in virtually any lesson plan, and design your lesson plans prepare your students for summative assessments.
Let’s dive into each of these.
Formative assessments are informal checks that help you monitor student progress throughout the lesson. They can include:
Formative assessments identify areas of student struggle and inform necessary adjustments to teaching methods to maintain lesson pace and student progress.
Summative assessments are used to evaluate student learning at the end of the unit. They can include:
Summative assessments provide insight into your students' mastery of the material and inform future lesson planning. They also help prepare students for standardized tests and ensure a strong foundation in the material.
Writing high-quality lesson plans is time-consuming for anybody. And as an educator there’s just so much that needs to be done in a day.
Good news: I’ve developed free, Common Core State Standards-aligned lesson plans that are easy to use in your class.

Each lesson plan includes objectives, time planning, relevant real-world applications and activities, detailed instructions, and answers to common student questions.
They’re a huge time-saver.

I spent 7 years in the classroom working to make math fun and relevant in middle school, by integrating math, art, and technology. I started Congruent Math to share this all with you.


September 23, 2023
December 17, 2023
Get my free resource library with digital & print activities—plus tips over email.